Topological sort

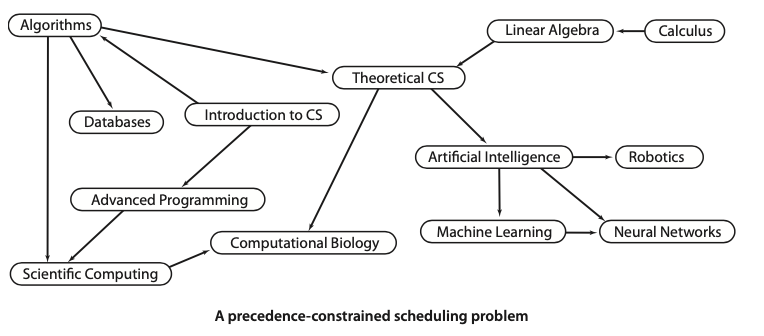
Topological Sort

• Topological Sort 是directed graph中解决precedence-constrained-scheduling 问题比较经典的算法。算法核心在于能否找到Directed-cycle
• A directed acyclic graph (DAG) is a digraph with no directed cycles.
• 比如大学选课系统，一些course需要prerequisite for certain other courses

Precedence-constrained scheduling: Given a set of jobs to be completed, with precedence constraints that specify that certain jobs have to be completed before certain other jobs are begun, how can we schedule the jobs such that they are all completed while still respecting the constraints?

public class DirectedCycle
  {
     private boolean[] marked;
     private int[] edgeTo;
     private Stack<Integer> cycle;
     private boolean[] onStack;
     public DirectedCycle(Digraph G)
     {
        onStack = new boolean[G.V()];
        edgeTo = new int[G.V()]; 
        marked = new boolean[G.V()]; 
        for (int v = 0; v < G.V(); v++)
            if (!marked[v]) dfs(G, v);
     }
     private void dfs(Digraph G, int v){
        onStack[v] = true;
        marked[v] = true;
        for (int w : G.adj(v))
        if (this.hasCycle()) return;
        else if (!marked[w]){// only when the vertex has not been visited  
            edgeTo[w] = v; dfs(G, w);  
        }else if (onStack[w]){
            cycle = new Stack<Integer>();
            for (int x = v; x != w; x = edgeTo[x])
                cycle.push(x); 
            cycle.push(w); 
            cycle.push(v);
        }
        onStack[v] = false;
    }
     public boolean hasCycle(){  
         return cycle != null;  
    }
     public Iterable<Integer> cycle(){
        return cycle;  
    }
}

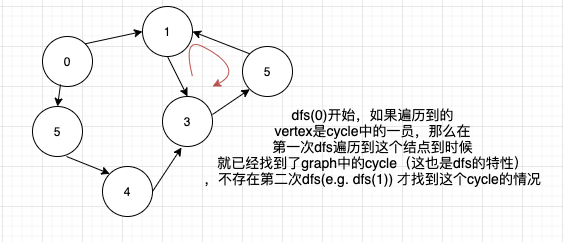
• !marked[w] 才会进行dfs的原因是，如果之前的dfs已经访问过当前vertex了，并且存在cycle的话，那么就已经找到cycle了

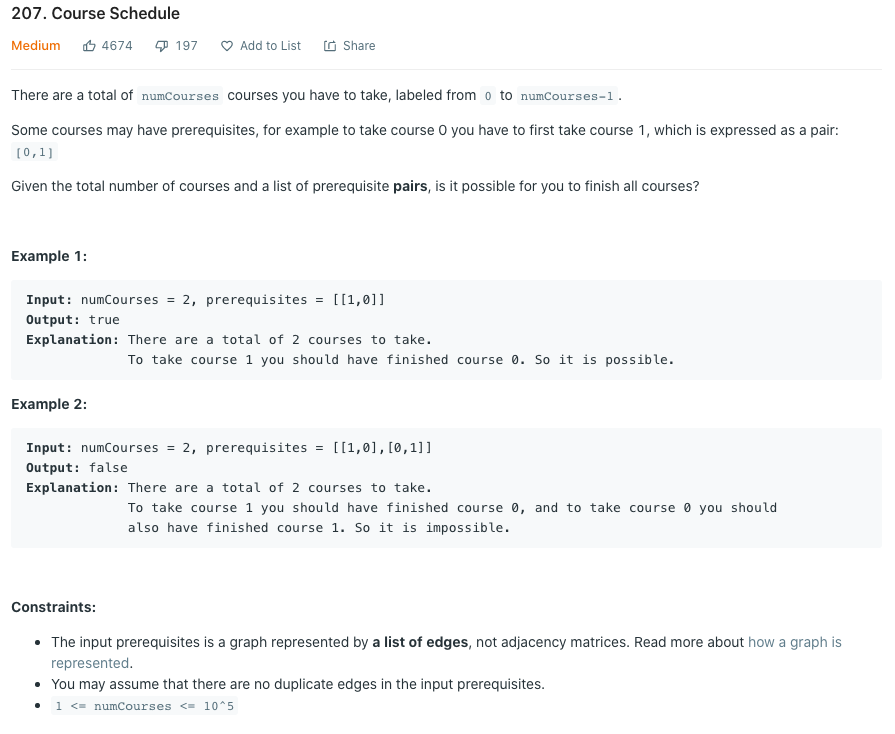
Leetcode 207. Course Schedule

class Solution {
    private boolean[] marked;
    private boolean[] stack;
    private Map<Integer, List<Integer>> graph = new HashMap<>();
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        marked = new boolean[numCourses];
        stack = new boolean[numCourses];
        for(int i = 0; i < prerequisites.length; i++){
            int pre = prerequisites[i][0];
            int nex = prerequisites[i][1];
            graph.computeIfAbsent(pre, (set) -> new ArrayList<>());
            graph.get(pre).add(nex);
        }
        
        for(int key : graph.keySet()){
            if(findDirectedCycle(key, graph.get(key)))
                return false;
        }
        
        return true;
    }
    
    private boolean findDirectedCycle(int w, List<Integer> vertexes){
        if(marked[w]) return false;
        if(stack[w]) return true;
        
        stack[w] = true;
        for(int vertex : vertexes){
            if(graph.containsKey(vertex) && findDirectedCycle(vertex, graph.get(vertex)))
                return true;
        }
        marked[w] = true;
        stack[w] = false;
        
        return false;
    }
}