IEEE 745 Floating-Point representation

    csapp   csapp  Comments

IEEE 745

在IEEE745统一浮点数表示方法之前，不同的计算机采用了不同的浮点数表示方法。

Floating-Point representation

  • The IEEE floating-point standard represents a number in a form $V = (−1)^s × M × 2^E$
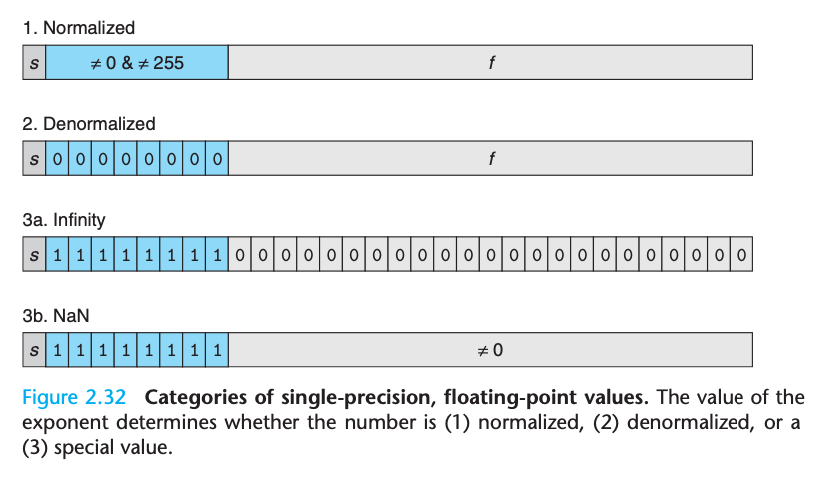
  • 如图s为0或者1，作为符号位; exp用来计算E 位数为 1)8bit–32位浮点数 2)11bit–64位浮点数; frac用来计算M 位数为 1)23bit–32位浮点数 2)52bit–64位浮点数
  • 不同的binary bit形式能够表示三种浮点数：
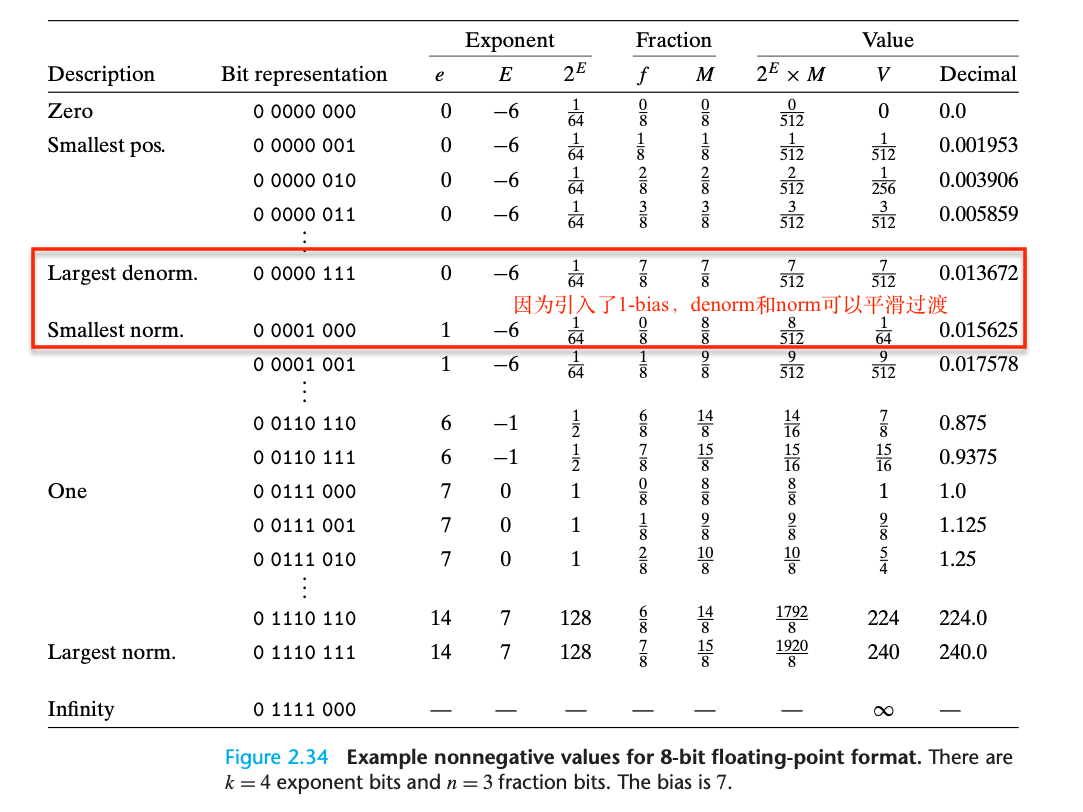
    • Normailized (exp 部分不全为0 || 不全为1)
      • $E = e - bias$ e为exp部分表示的unsgined数的值，$bias=2^(k-1) - 1$ k为exp部分的位数(8–32位浮点数， 11–64位浮点数)
      • $M = [1.f_{n-1}, f_{n-2}, f_{n-3}… f_0]$ fn-1, fn-2表示的是 frac 部分每一个bit上的值(0或者1) $f = f_{n-1} * 2^{-1} + f_{n-2} * 2^{-2} + … + f_0 * 2^{-n}$ and $0 \leq f < 1$
    • Denormalized (exp 部分全为0)
      • $E = 1 - bias$
      • $M = [0.f_{n-1}, f_{n-2}, f_{n-3}… f_0]$ 此时M没有leading 1 $0 \leq M < 1$
      • denormalized 可以表示0和非常接近0的小数(E为一个绝对值很大的负数)
    • Special Value (exp 部分全为1)
      • 如果frac部分全为0，s为0表示$+ \infty$
      • 如果frac部分全为0，s为1表示$- \infty$
      • 如果frac部分不为0，则表示NAN “not a number” (除0)

about IEEE 745

  • 为什么用unsigned值来解码exp部分:这是为了浮点数大小比较的方便。使用unsigend值，如果符号位为0，只需要按位比较就可得到比较结果。如果用signed值表示exp部分的话，考虑exp使用4bit,这样的话1000代表-8，0111代表7，$2^{7} > 2^{-8}$但是$0111 < 1000$这样大小比较的时候就需要即考虑frac部分又考虑exp部分。即使s符号位为1使用unsgined解码exp部分，只需要将除符号位以外的bit大小比较的结果取反就可以了
  • 为什么使用bias: 因为使用了unsgined解码exp部分，需要将exp所取的unsgined值的区间做偏移，这样既可以表示一个小数点后位数很多的数(当E是一个绝对值很大的负数)，也可以表示一个绝对值很大的数(当E是一个很大的正数)
  • 为什么denormalized情况下$E = 1-bias$而不是$E = -bias$: 这是为了denormalized与normalized的边界点能够平滑过渡。denormalized跨到normalized的第一个值的exp部分一定是00..001,$E = e - bias = 1 - bias$

Mark ZhangSoftware Engineer

Hi there ~