Bitwise operations
- | OR
- & AND
- ^ XOR
- ~ Bitwise Complement: it makes every 0 to 1, and every 1 to 0.
- right shift >> left shift << e.g. x = 00111011; x >> 2; x = 00001110
- -n = ~n + 1
Common use
- a^b^b = a
- 0^a = a^0 = a
- a^a = 0
- N&(-N) merely keeps the rightmost 1 bit (equals N & (~N + 1))
- N&(N - 1) remove the rightmost 1
- The >>> operator is the unsigned right bit-shift operator (no matter the leftmost bit is 1 or 0, automatically add 0 to the left)
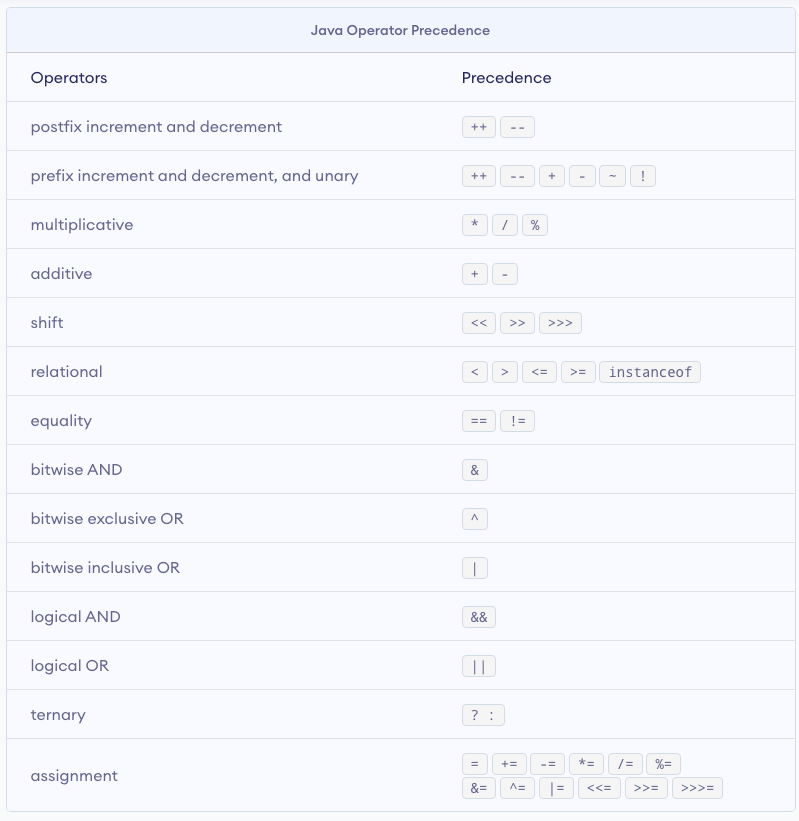
Java operator precedence
leetcode problems
- Single Number II
Given a non-empty array of integers, every element appears three times except for one, which appears exactly once. Find that single one.
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?
Input: [2,2,3,2] Output: 3 Input: [0,1,0,1,0,1,99] Output: 99
- Solution
- 将array中所有数值按位加合,与3做余数计算,得到的结果必定是0或者1
- 按位与0做XOR计算得出single number
class Solution {
public int singleNumber(int[] nums) {
int res = 0;
//int has 32 bits in Java
for(int i = 0; i < 32; i++){
int sum = 0;
for(int j = 0; j < nums.length; j++){
//count number of '1' at each position
sum += nums[j] >> i & 1;
}
// the result of sum % 3 is 0 or 1
res ^= (sum % 3) << i;
}
return res;
}
}
- Counting Bits
Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1’s in their binary representation and return them as an array.
Example 1:
Input: 2 Output: [0,1,1]
Example 2:
Input: 5 Output: [0,1,1,2,1,2]
Follow up:
It is very easy to come up with a solution with run time O(n*sizeof(integer)). But can you do it in linear time O(n) /possibly in a single pass?
Space complexity should be O(n).
Can you do it like a boss? Do it without using any builtin function like __builtin_popcount in c++ or in any other language.
- Solution
- 对于每一个 0 <= i <= nums, 移除最右边的1所得到的十进制的值的hamming weight + 1 即当前i值的hamming weight
class Solution {
//dp time complexity O(n) | space complexity O(1)
public int[] countBits(int num) {
//res[i] represents the popcount(hamming weight) of i
int[] res = new int[num + 1];
for(int i = 1; i <= num; i++)
//remove the rightmost 1
res[i] = res[i&(i-1)] + 1;
return res;
}
}
- Reverse Bits
Reverse bits of a given 32 bits unsigned integer.
Example 1:
Input: 00000010100101000001111010011100 Output: 00111001011110000010100101000000
Example 2:
Input: 11111111111111111111111111111101 Output: 10111111111111111111111111111111
public class Solution {
// you need treat n as an unsigned value
public int reverseBits(int n) {
int pos = 31;
int res = 0;
while(n != 0){
//precedence of += is lower than & and <<
res += (n & 1) << pos;
n =>>> 1;
pos --;
}
return res;
}
}
- Bitwise AND of Numbers Range
Given a range [m, n] where 0 <= m <= n <= 2147483647, return the bitwise AND of all numbers in this range, inclusive.
Example 1:
Input: [5,7] Output: 4
Example 2:
Input: [0,1] Output: 0
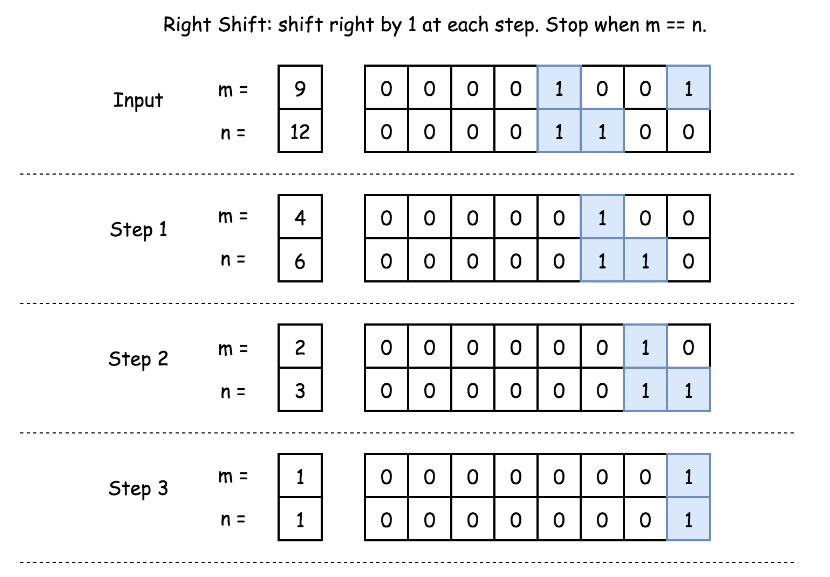
- solution
- 找到 m 和 n的common prefix
class Solution {
public int rangeBitwiseAnd(int m, int n) {
int count = 0;
while(m != 0){
if(m == n)
break;
m >>= 1;
n >>= 1;
count ++;
}
return m << count;
}
}
